ページ番号:114774
掲載日:2024年7月11日
ここから本文です。
円グラフ(えんグラフ)
円グラフってどんなグラフ?
 コバトンのセリフ1
コバトンのセリフ1
割合(わりあい)を表すグラフと言えば、帯グラフ(おびグラフ)のほかに「円グラフ(えんグラフ)」があるね。
円グラフも小学校5年生で習うよ。
次の統計表を円グラフにしてみるよ。
| 血液型 | A型 | O型 | B型 | AB型 |
| 人数(人) | 24 | 18 | 12 | 6 |
| 割合(%) | 40 | 30 | 20 | 10 |
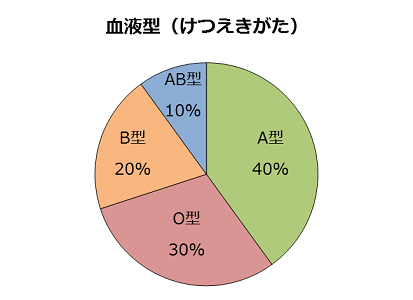
こんなふうに、円グラフは、円の中心からおうぎ形に円を区切って、おうぎ形の中心角の大きさで割合を表したものなんだ。おうぎ形の中心角の大きさと、おうぎ形の面積は比例(ひれい)するから、おうぎ形の面積で割合を表したものとも言えるね。
円グラフと百分率
 コバトンのセリフ2
コバトンのセリフ2
円グラフでも、割合(わりあい)の大きさを数字で表す場合はふつう百分率(ひゃくぶんりつ)を使うんだけど、じっさいにグラフを作るのは帯グラフよりもむずかしくなるよ。
帯グラフの場合、たとえば帯の長さを100ミリメートルにすれば、1パーセントは1ミリメートルになるから、じょうぎを使えば割合を区切っていくのはそんなにむずかしくないよね。
いっぽう、円グラフの場合、円の中心角360度を100パーセントとして表すから、1パーセントは3.6度になるよ。でもふつうの分度器には0.1度のめもりは付いていないから、目分量で書かないといけない。角度1度の小さなめもりをさらに10等分して正しく書くのはむずかしいし、小数の計算も必要になる。小学校の高学年にならないと、正しく書くのはむずかしいグラフと言えるね。百分率のめもりの付いた百分率全円分度器というものもあるけど、ふつうは持っていないしね。
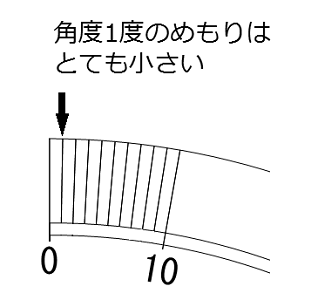
でも、あきらめることはないよ。身の周りの「あるもの」を使えば、百分率の計算を知らない小学校4年生以下でも円グラフを作れる場合があるんだ。
百分率を使わない円グラフ
 コバトンのセリフ3
コバトンのセリフ3
身の周りの「あるもの」とはズバリ、時計の文字盤(もじばん)だよ。1時間は60分だから、60このめもりが付いている時計をヒントにすれば、百分率(ひゃくぶんりつ)や角度の計算を知らなくても円グラフのようなグラフを作れる場合があるんだ。
たとえば60人にアンケートをした場合なら、24人は24分、18人なら18分というように1人を1分と考えて円を区切れば、計算しなくても円グラフのようなグラフが作れるね。このやりかたは、60人、30人、20人、15人、12人、10人、6人、5人、4人、3人、2人の場合にしか使えないけどね。
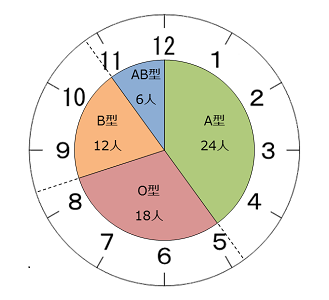
もう一つ、紙を折って作るやりかたもあるよ。おりがみを半分、また半分、また半分、また半分、また半分というように折ってできた折り目を使えば、2人、4人、8人、16人、32人の場合を表すことができるんだ。
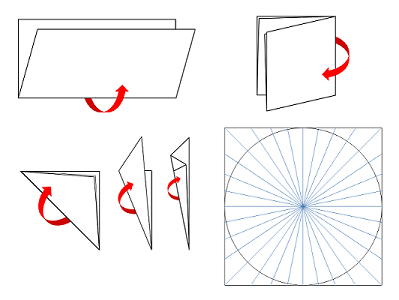
低学年なら、そんなに大きな数を使うことはないだろうから、うまく数が合えばためしてみてもいいかもしれないね。
円グラフの書きかた
 コバトンのセリフ4
コバトンのセリフ4
円グラフは、これまで見てきたグラフのように、直線じょうぎだけでは書けないから、ここで書きかたをおさらいしておこう。
統計表を作る
まずはグラフの元になる統計表をしっかり作ろう。
| 血液型 | A型 | O型 | B型 | AB型 | 合計 |
| 人数(人) | 60 | 45 | 30 | 15 | 150 |
| 割合(%) | 40 | 30 | 20 | 10 | 100 |
| 角度 | 144 | 108 | 72 | 36 | 360 |
ポイントの一つは角度を計算して書くことだよ。1パーセントは3.6度に当たるから、パーセントで表した割合(わりあい)の数に3.6をかけて角度を計算しよう。たとえば40パーセントなら、40かける3.6で144度になるよ。
もう一つのポイントは角度の合計を計算することだよ。これは、合計が360度になるかどうか検算するためなんだ。角度の計算はどうしても小数の計算になるから、計算ミスをしやすいからね。
円を書く
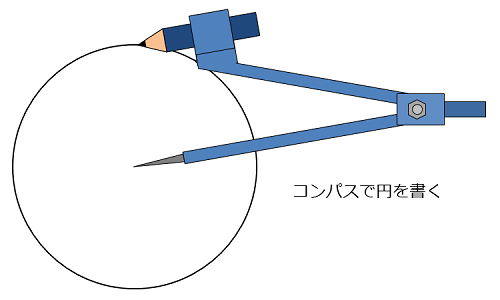
コンパスで作りたい大きさの円を書こう。
円グラフを書くときには円の中心が必要だから、コンパスを使うといいんだ。コンパスなら、はりあなが円の中心になるよ。
始まりの0の線を書く
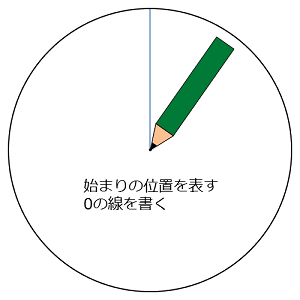
始まりの位置を表す0(ゼロ)の線を書こう。
ふつうは、時計の12時に当たる位置を0にするよ。中心から真上に向かう直線を引こう。この線が始まりの0の線になるよ。
角度をはかって円を区切る
0の線から角度をはかって円を区切っていこう。
ふつうは、時計回りに順番に区切っていくよ。分度器の中心を円の中心に合わせ、分度器の0度のめもりを0の線に合わせて角度をはかろう。
今回の場合だと144度のめもりに目印を付ければいいね。

そして円の中心から目印に向かって直線を引いて、おうぎ形に円を区切ろう。次はこの線に0度のめもりを合わせて角度をはかることになるよ。今回の場合だと次は108度だね。
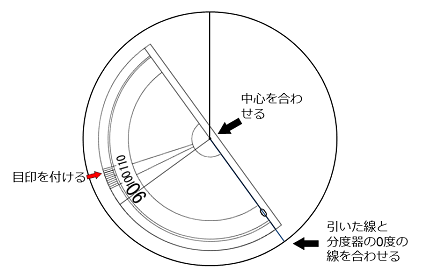
この作業をくり返して順番に円を区切っていくんだ。
割合の大きさを数字で書く
最後にそれぞれの割合の大きさを数字で書こう。ふつうは百分率(ひゃくぶんりつ)、つまりパーセントで表すよ。
今回の場合だと40%、30%、20%、10%というように書けばいいね。
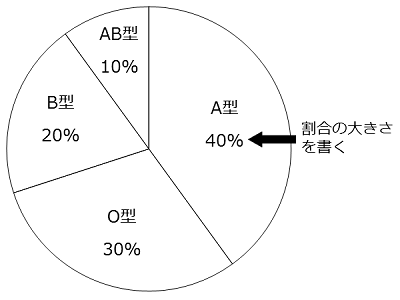
角度の大きさを読み取るのは、長さとちがって意外にむずかしいから、円グラフの場合は必ず数字を書きそえるようにしよう。
これで円グラフのできあがりだよ。
円グラフと帯グラフ
コバトンのセリフ5
今おさらいしたように、円グラフは書くのに手間がかかるよね。じょうぎのほかにコンパスや分度器も必要だし。
割合(わりあい)を表すならもっとかんたんに書ける帯グラフでもいいのに、どうしてわざわざ円グラフを作るんだろう?きっと円グラフを作る理由があるはずだよね。
次は帯グラフとくらべながら、その理由を見ていこう。
円グラフの特ちょう1
 コバトンのセリフ6
コバトンのセリフ6
円グラフの特ちょうの一つが、「形が丸いこと」だよ。
 男の子、はかるのセリフ1
男の子、はかるのセリフ1
円なんだから、そんなの当たり前じゃない。
 コバトンのセリフ7
コバトンのセリフ7
そう、円が丸いのは当たり前だけど、それが重要なんだ。
いままで見てきた棒グラフ、折れ線グラフ、帯グラフのように、統計グラフは直線でできているものが多いから、円グラフの丸い形は、その中で目を引くという良さがあるんだ。帯グラフは長方形だから、棒グラフなどと同じような感じになってしまうからね。
特に統計グラフコンクールの作品のように、たくさんのグラフをならべる場合、円グラフをまぜると見た目の変化を付けることができるよ。
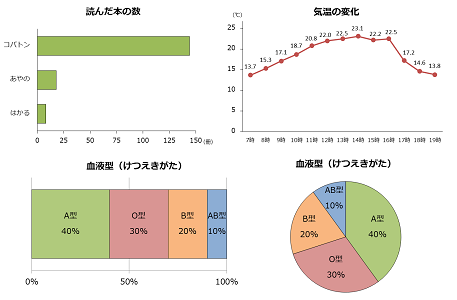
円グラフの特ちょう2
 コバトンのセリフ8
コバトンのセリフ8
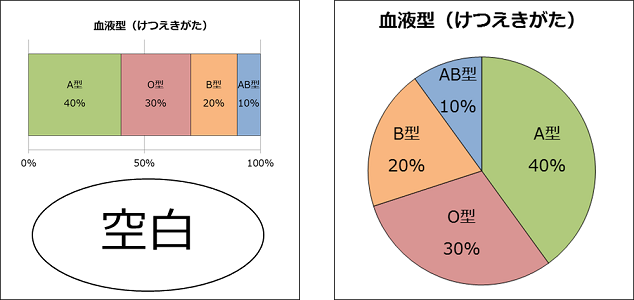
円グラフのもう一つの特ちょうが、「正方形のスペースにぴったり書ける」ことだね。
帯グラフは、せまいスペースに大きく書ける良さがあるという話をしたけど、正方形のスペースだと反対に空白が大きくてなってしまうんだ。
帯グラフと円グラフのどちらを使っても問題ないときは、グラフを書くスペースの形で選んでもいいね。
円グラフの特ちょう3
 コバトンのセリフ9
コバトンのセリフ9
円グラフには、「半分より多いか少ないかがひと目で分かる」という特ちょうもあるよ。
たとえば次のグラフはわざと数字をいれていないんだけど、帯グラフのほうは、「よい」のほうが「わるい」より多いことは分かるけど、「よい」が半分より多いか少ないかは、ちょっと分かりにくいよね。
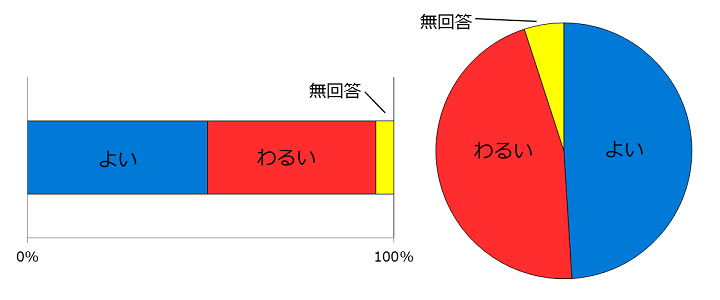
でも円グラフのほうは、「よい」が多いということだけでなく、半分よりちょっと少ないということまでひと目で分かるよね。
だから、「半分より多いか少ないか」を分かりやすく伝えたい場合に円グラフがよく使われるんだ。たとえば選挙のニュースなどがそうだね。
円グラフの弱点1
 コバトンのセリフ10
コバトンのセリフ10
ほかのグラフにはない特ちょうのある円グラフだけど、弱点もいくつかあるんだ。
その一つがさっきおさらいしたように「書くのに手間がかかる」ことだよ。
 女の子、あやののセリフ1
女の子、あやののセリフ1
そうね。コンパスや分度器などの道具も使わないといけないし。
 コバトンのセリフ11
コバトンのセリフ11
だから、統計データを読み取るために割合(わりあい)のグラフを作るときは、まずは帯グラフを作ってみることをおすすめするよ。
帯の長さを100ミリメートルにすれば、1ミリメートルを1パーセントとしてすぐに割合のグラフが書けるからね。
とりあえず作るという目的には、円グラフは手間がかかりすぎて合っていないんだ。
円グラフの弱点2
 コバトンのセリフ12
コバトンのセリフ12
もう一つ円グラフの弱点として、「うちわけの数が多いとくらべにくい」ことがあるよ。
さっきまでは円グラフの良さを見るために、うちわけの数が四つまでのグラフしか出さなかったけど、次のような円グラフはどうかな?
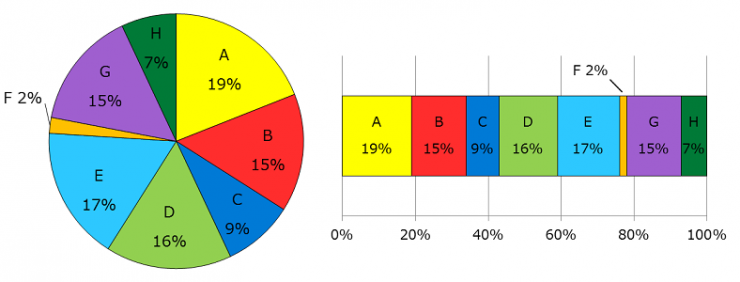
 男の子、はかるのセリフ2
男の子、はかるのセリフ2
うひゃー、目がチカチカするよ。うちわけが八つもあるのか。
 コバトンのセリフ13
コバトンのセリフ13
円グラフのAとEをくらべたときにどちらの割合(わりあい)多いかひと目で分かるかな?
 女の子、あやののセリフ2
女の子、あやののセリフ2
数字が書いてなかったら、ひと目ではむずかしいと思うわ。
 コバトンのセリフ14
コバトンのセリフ14
そうだね、苦労して円グラフを作ったのに、あまり分かりやすくないよね。
うちわけの大きさをくらべるなら、となりの帯グラフのほうがずっと見やすくていいよね。
これは角度のわずかなちがいを見分けるのは、長さの場合よりもむずかしいからなんだ。
円グラフの場合、うちわけの数が多くなるほど、おうぎ形の角度のわずかなちがいを読み取らなくてはいけないことになるから、「うちわけの数が多い」ものはあまり円グラフに向いていないんだ。
円グラフの弱点3
 コバトンのセリフ15
コバトンのセリフ15
「グラフどうしをくらべるのがむずかしい」というのも円グラフの弱点だね。
次の図はグラフを四つならべてくらべた場合だけど、帯グラフをならべたほうは、割合(わりあい)の変化のようすがとてもよく分かるね。
それに対して円グラフをならべたほうは、変化のようすを読み取るのにちょっと苦労しそうだよね。
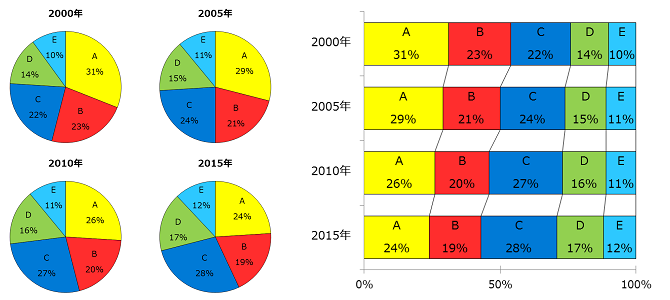
これは、はなれた所にある角度のわずかなちがいを読み取るのが人間にはむずかしいからなんだ。
たった四つならべた場合でこれだから、グラフの数が七つ、八つと多くなったらもっとくらべるのが大変になってしまうね。
そういうわけで、円グラフは「グラフどうしをくらべる」のに向いていないんだ。
円グラフを作るときに注意すること
 コバトンのセリフ16
コバトンのセリフ16
それじゃあ円グラフを作るときに注意するポイントを見ていこう。
円グラフのポイントは、帯グラフの場合と共通する所が多いんだ。
うちわけが何を表しているかの説明を必ず書こう
どれが何を表しているのか分かるように必ず説明を書こう。
用語の説明:統計グラフで使われている棒や線、色やもようが何を表しているかを説明する注意書きを「凡例(はんれい)」といいます。凡例がないとグラフを正しく読むことができません。必ず凡例を書きましょう。
うちわけは数の大きい順にならべよう
これは帯グラフと同じだね。順番に意味があるときはその順番にならべることや、「その他」があるときは最後に書くことも同じだよ。
うちわけの合計は100%
これも帯グラフと同じで内訳の合計は100%になるよ。計算ミスや書きまちがいで100%になっていないことが意外に多いから書くときはよく注意してね。
うちわけの合計が100%にならないとき
四捨五入(ししゃごにゅう)したため、うちわけの合計が100%にならなくなった場合の考えかたも帯グラフといっしょだよ。
0.1%のちがいは角度にすると0.36度のちがいになるけど、0.36度のめもりの長さは直径10センチメートルの分度器の場合で、たった0.3ミリメートルにしかならないんだ。ふつうの大きさの円グラフなら十分正確(せいかく)なグラフが作れるよ。
円グラフのまとめ
 コバトンのセリフ17
コバトンのセリフ17
見てきたように円グラフは、他の種類のグラフにない良い所もあるけど、弱点もまた多いグラフなんだ。
だから、使う前に本当に円グラフで表すのに向いているかどうかよく考えてから使うようにしよう。
うちわけが多いときや、ほかとくらべることに重点がある場合は、円グラフより帯グラフのほうが向いているよ。

