ページ番号:114628
掲載日:2024年7月11日
ここから本文です。
帯グラフ(おびグラフ)
帯グラフってどんなグラフ?
 コバトンのセリフ1
コバトンのセリフ1
次は割合(わりあい)を表すときに使う「帯グラフ(おびグラフ)」を見ていこう。
帯グラフは小学校5年生で習うよ。
次の統計表を帯グラフにしてみるよ。
| 血液型 | A型 | O型 | B型 | AB型 |
| 人数(人) | 60 | 45 | 30 | 15 |
| 割合(%) | 40 | 30 | 20 | 10 |
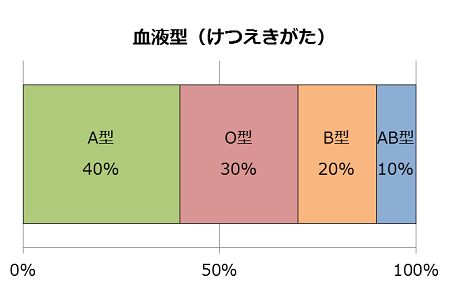
こんなふうに、帯グラフは、割合を長方形のはばで表したものなんだ。
統計で割合を表すときは、ふつう百分率(ひゃくぶんりつ)を使うんだけど、百分率という言葉は初めて聞くかな?でも、パーセント(%)なら聞いたことがあるよね。実はパーセントというのは、百分率で割合を表したものなんだよ。
百分率も小学校5年生で習うんだけど、百分率を計算して帯グラフを作るのは、習った後でないとちょっとむずかしいかもしれないね。
でも、あきらめることはないよ。百分率の計算を知らない3年生や4年生でも、棒グラフを変形させれば帯グラフに近いものを作ることができるからね。次はそのやりかたを見ていこう。
帯グラフと棒グラフ1
 コバトンのセリフ2
コバトンのセリフ2
それじゃあ、棒グラフを変形させて帯グラフのようにしてみるよ。
まず統計表からふつうに棒グラフを作って、
| 季節名 | 春 | 夏 | 秋 | 冬 |
| 人数(人) | 4 | 15 | 5 | 6 |
| 割合(%) | 13.3 | 50.0 | 16.7 | 20.0 |
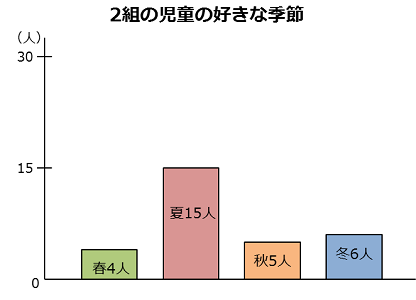
次にすべての棒を1か所に積み上げて、
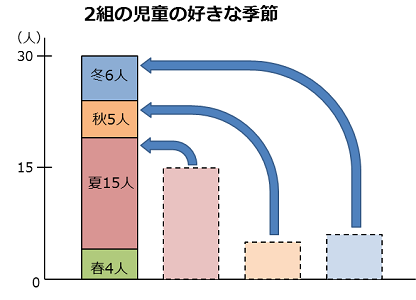
最後に棒のはばを見やすく調整すれば積み上げ棒グラフのできあがり。
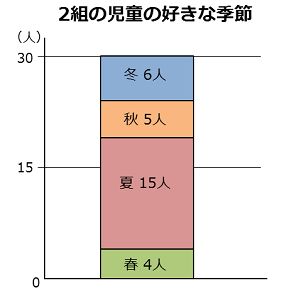
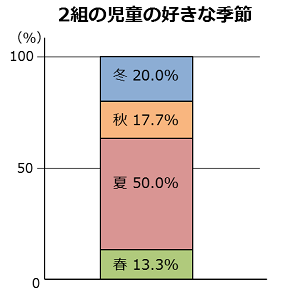
となりに、はばと高さが同じ帯グラフも作ってみたよ。二つをくらべると、単位がちがうだけで、ほかはまったく同じだよね。
こんなふうに棒グラフをくふうすれば、帯グラフのように割合(わりあい)をグラフの形で見えるようにできるんだ。さすが統計グラフの基本(きほん)、棒グラフだね。
それなら、どうして積み上げ棒グラフでも表すことができるのに、わざわざ百分率の計算をして帯グラフを作るんだろうね?きっと帯グラフを作る理由があるはずだよね。次は積み上げ棒グラフとくらべながら、その理由を見ていこう。
帯グラフと棒グラフ2
 コバトンのセリフ3
コバトンのセリフ3
さて今度は、次の統計表を積み上げ棒グラフにして、割合(わりあい)を表してみるよ。
| 季節名 | 春 | 夏 | 秋 | 冬 |
| 人数(人) | 6 | 16 | 5 | 7 |
| 割合(%) | 17.6 | 47.1 | 14.7 | 20.6 |
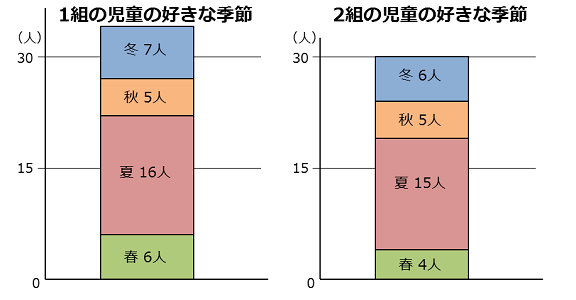
となりに2組の児童の場合をならべてみたけど、二つのグラフをくらべてみてどうかな?1組のほうが人数が多いのは一目で分かるけど、ここで知りたいのは数の大きさじゃなくて割合だよね。
それでは、夏が好きな人、1組の16人と2組の15人、割合が大きいのはどちらか一目でパッと分かるかな?意外にむずかしいよね。
計算すると1組は34人だから16人は半分より少ないね。2組は30人だから15人はちょうど半分。1組の16人のほうが割合が大きいようにも見えるけど、2組の15人のほうが割合が大きかったんだね。
こんなふうに、積み上げ棒グラフの場合は、ほかのグラフと割合をくらべるのがむずかしいという弱点があるんだ。
 男の子、はかるのセリフ1
男の子、はかるのセリフ1
それなら、めもりのはばをくふうして積み上げたときの棒の高さを同じにすればいいんじゃない?
 コバトンのセリフ4
コバトンのセリフ4
そうだね、棒の高さが同じならくらべやすそうだね。
じゃあ、じっさいに34人のグラフを30人のグラフの高さに合わせて、高さをちぢめるにはどうすればいいだろう?
 女の子、あやののセリフ1
女の子、あやののセリフ1
34を30にすればいいんだから、それぞれの人数を34でわって30をかければいいと思うわ。34を34でわると1で、1に30をかければ30になるでしょ。
 コバトンのセリフ5
コバトンのセリフ5
さすがあやのくん、そのとおり。1組の春夏秋冬それぞれの人数を34でわって30をかければいいんだ。計算のようすを表にするとこうなるよ。
| 季節名 | 春 | 夏 | 秋 | 冬 |
| 人数(人) | 6 | 16 | 5 | 7 |
| 34でわると | 0.17647 | 0.47059 | 0.14706 | 0.20588 |
| 30をかけると | 5.294 | 14.118 | 4.412 | 6.176 |
じゃあ反対に30人のグラフを34人のグラフに合わせるにはどうすればいいかな?
 女の子、あやののセリフ2
女の子、あやののセリフ2
同じように考えれば、30を34にすればいいんだから、30でわって34をかければいいと思うわ。
 コバトンのセリフ6
コバトンのセリフ6
そうだね。2組の春夏秋冬それぞれの人数を30でわって34をかければいいんだ。同じく計算のようすを表にするとこうなるよ。
| 季節名 | 春 | 夏 | 秋 | 冬 |
| 人数(人) | 4 | 15 | 5 | 6 |
| 30でわると | 0.13333 | 0.5 | 0.16667 | 0.2 |
| 34をかけると | 4.533 | 17 | 5.667 | 6.8 |
 男の子、はかるのセリフ2
男の子、はかるのセリフ2
ちょっと待って。二人ともさらっと話を進めているけど、その計算をしてグラフを作るのってかんたんじゃないよね。わりきれない小数は出てくるし。そもそも百分率(ひゃくぶんりつ)の計算を知らない3年生や4年生でも、積み上げ棒グラフならできるって話じゃなかったっけ?これじゃ百分率の計算をするよりもややこしいよ!
 コバトンのセリフ7
コバトンのセリフ7
はかるくんの言うことはもっともだね。
でもここは帯グラフの特ちょうの話だからそれはちょっと置いといて先に進めるよ。「ややこしい計算」をして棒の高さを同じにするとこうなるよ。
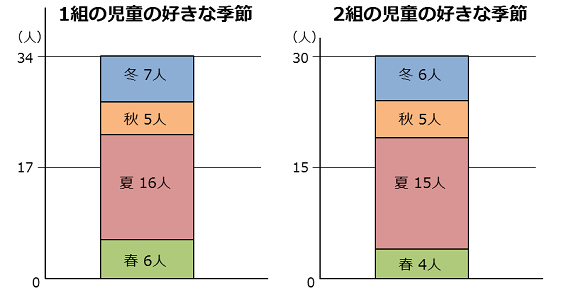
 男の子、はかるのセリフ3
男の子、はかるのセリフ3
うーん、棒だけ見ればくらべやすくなったけど、34人と30人のめもりのはばが同じだと、まちがえて作ったみたいでなんだか気持ち悪いね。グラフの中に書いてある人数もくらべづらいし。自分で言い出しておいてなんだけど、思ったよりくらべやすくない気がする。
 コバトンのセリフ8
コバトンのセリフ8
はかるくん、正直な感想ありがとう。
「ややこしい計算」をして棒の高さをそろえても、やっぱり積み上げ棒グラフの場合は割合(わりあい)をくらべるのがむずかしいようだね。
ここでは説明のために、34人と30人のグラフの高さを同じにそろえたけど、棒グラフの場合、34人と30人のように単位が同じで大きさがちがうものを同じ長さで表してならべることはないよ。だから、はかるくんの心配した「ややこしい計算」をすることもじっさいはないから安心していいよ。
さて、帯グラフの良さを言うために、積み上げ棒グラフの話が長くなったね。ここでやっと帯グラフの登場だよ。1組と2組の「児童の好きな季節」の割合を帯グラフで表してみるよ。
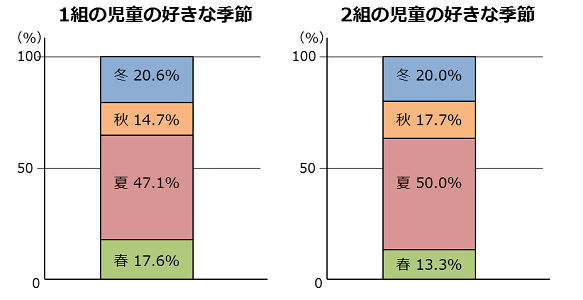
 女の子、あやののセリフ3
女の子、あやののセリフ3
棒の色や大きさはまったく同じなのに、割合(わりあい)のくらべやすさが全然ちがうわ。34人のうち7人と言われても、ピンと来なかったけど、100%のうちの20.6%ならすぐに割合の大きさが分かるもの。
 コバトンのセリフ9
コバトンのセリフ9
そうだね。割合(わりあい)を表すために考え出されたグラフなんだから当たり前だけど、あやのくんの言うとおり、帯グラフのほうがずっと分かりやすいね。
一つの帯グラフの中の数字もくらべやすいし、ほかの帯グラフともくらべやすい。これが積み上げ棒グラフよりすぐれた特ちょうだね。だからわざわざ百分率(ひゃくぶんりつ)の計算をして帯グラフを作るんだね。
帯グラフの特ちょう1
 コバトンのセリフ10
コバトンのセリフ10
帯グラフは割合(わりあい)を表すグラフの基本(きほん)だよ。百分率(ひゃくぶんりつ)の計算ができるようになったあと、割合を表すグラフを作りたいときは、まずは帯グラフを作ってみて、そこからくふうを始めるといいよ。
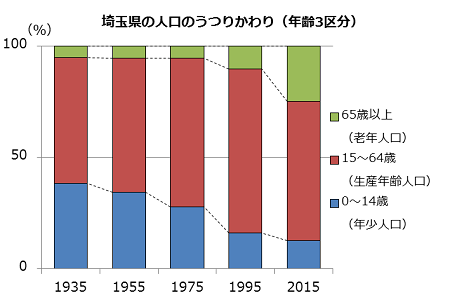
特に帯グラフは、次の「埼玉県の人口のうつりかわり」のグラフのように二つ、三つとグラフをならべてくらべるのに向いているよ。0~14歳の子どもの割合が小さくなっていくようすがよく分かるね。
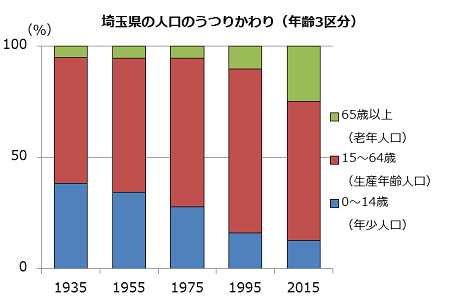
積み上げ棒グラフには、割合と同時に数の大きさも表すことができるという帯グラフにはない特ちょうがあるよ。同じ「埼玉県の人口のうつりかわり」を、積み上げ棒グラフにしてみるよ。
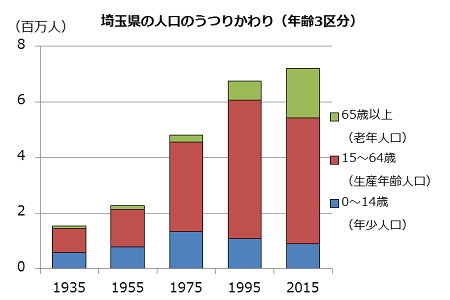
0~14歳の子どもの割合は小さくなっていくけど、人数はそれほどへっていないことが分かるね。帯グラフと積み上げ棒グラフ、それぞれに特ちょうがあるから、場面によって使い分けるといいね。
帯グラフの特ちょう2
 コバトンのセリフ11
コバトンのセリフ11
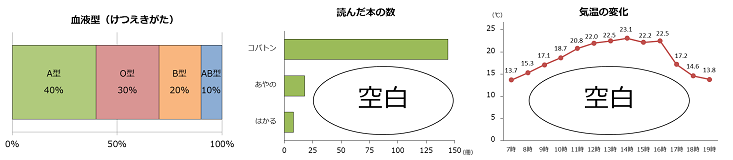
帯グラフのもう一つの特ちょうが、せまいスペースでも大きくて見やすいグラフが書けることだね。棒グラフや折れ線グラフは、空白が大きくて主役の棒や折れ線が小さくなってしまうことがあるけど、帯グラフは空白ができないからスペースいっぱいに大きく帯を書くことができるからね。
帯グラフを作るときに注意すること
 コバトンのセリフ12
コバトンのセリフ12
それじゃあ帯グラフを作るときに注意するポイントを見ていこう。
帯グラフのポイントは、棒グラフや折れ線グラフの場合と共通することが多いんだ。
必ず始まりの0(ゼロ)を書こう
棒グラフや折れ線グラフと同じだね。
目もりのはばを正しくそろえよう
これも棒グラフや折れ線グラフと同じだね
帯をならべるときは帯と帯のかんかくをそろえよう
棒グラフの棒のかんかくをそろえるのと同じだね。
帯のうちわけが何を表しているかの説明を必ず書こう
どれが何を表しているのか分かるように必ず説明を書こう。
用語の説明:統計グラフで使われている棒や線、色やもようが何を表しているかを説明する注意書きを「凡例(はんれい)」といいます。凡例がないとグラフを正しく読むことができません。必ず凡例を書きましょう。
帯のうちわけは数の大きい順にならべよう
これは棒グラフと同じだね。順番に意味があるときはその順番にならべることや、「その他」があるときは最後に書くことも同じだよ。
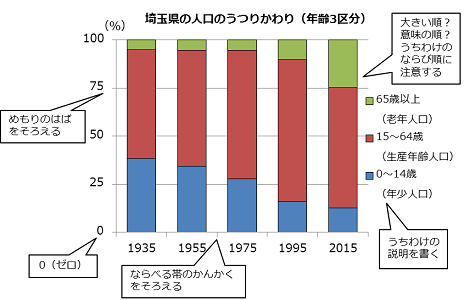
うちわけどうしを線で結ぶ
 コバトンのセリフ13
コバトンのセリフ13
帯グラフをならべて、割合(わりあい)の変化のようすを見るときは、同じうちわけどうしを少し細めの線や点線で結んで、同じものであることを強調することがあるよ。
うちわけの合計は100%
 コバトンのセリフ14
コバトンのセリフ14
帯グラフのうちわけの合計は100%になるよ。
 男の子、はかるのセリフ4
男の子、はかるのセリフ4
百分率(ひゃくぶんりつ)なんだから、そんなの当たり前じゃない。
 コバトンのセリフ15
コバトンのセリフ15
当たり前なんだけど、計算ミスや書きまちがいで100%になっていないことが意外に多いんだ。書くときはよく注意してね。
うちわけの合計が100%にならないとき1
 女の子、あやののセリフ4
女の子、あやののセリフ4
そうそう、計算ミスじゃないんだけど、わり切れない数を四捨五入(ししゃごにゅう)したら、合計が99.9%や100.2%になってしまった場合はどうするの。今作っているグラフでも100%にならなくてこまっているんだけど。
 コバトンのセリフ16
コバトンのセリフ16
四捨五入(ししゃごにゅう)したら合計が100%にならないことはよくあるね。次のような場合だね。
| (人) | 四捨五入前(%) | 四捨五入後(%) | |
| 春 | 10 | 33.33333 | 33.3 |
| 夏 | 7 | 23.33333 | 23.3 |
| 秋 | 6 | 20 | 20 |
| 冬 | 4 | 13.33333 | 13.3 |
| その他 | 3 | 10 | 10 |
| 合計 | 30 | 100 | 99.9 |
| (人) | 四捨五入前(%) | 四捨五入後(%) | |
| 春 | 11 | 34.375 | 34.4 |
| 夏 | 6 | 18.75 | 18.8 |
| 秋 | 10 | 31.25 | 31.3 |
| 冬 | 3 | 9.375 | 9.4 |
| その他 | 2 | 6.25 | 6.3 |
| 合計 | 32 | 100 | 100.2 |
やりかたはいくつかあるけど、埼玉県の統計課では次のように、合計だけ100%に直して、「四捨五入のため、うちわけの合計は100%にならない場合がある」のような注意書きを入れているよ。
| (人) | (%) | |
| 春 | 11 | 34.4 |
| 夏 | 6 | 18.8 |
| 秋 | 10 | 31.3 |
| 冬 | 3 | 9.4 |
| その他 | 2 | 6.3 |
| 合計 | 32 | 100 |
注意:四捨五入のため、うちわけの合計は100%にならない場合がある
うちわけの合計が100%にならないとき2
 コバトンのセリフ17
コバトンのセリフ17
合計が合わないなんて気持ち悪い、どうしても合計を100%にしたいときは、影響(えいきょう)の少ない所で調整するんだ。
例えば100.3%だったら、まず「その他」から0.1を引く、次に「割合(わりあい)の一番大きい所」から0.1を引く、その次に「二番目に大きい所」から0.1を引く、というように順番に調整していくのがふつうだね。
でもいつも「一番大きい所」で調整すれば良いとも限らないんだ。例えばさっきの「合計が100.2%になった例」の場合は、次の表のように「その他」と二番目に大きい「秋31.3%」の2か所で調整したほうが影響が少なくてすむよ。
| (人) | 四捨五入前(%) | 調整後(%) | 四捨五入前と調整後の差 | |
| 春 | 11 | 34.375 | 34.4 | |
| 夏 | 6 | 18.75 | 18.8 | |
| 秋 | 10 | 31.25 | 31.2 | 0.05 |
| 冬 | 3 | 9.375 | 9.4 | |
| その他 | 2 | 6.25 | 6.2 | 0.05 |
| 合計 | 32 | 100 | 100 |
表を見ると、四捨五入(ししゃごにゅう)する前と調整した後の「秋」の差は0.05だよね。もし「春」を調整して34.3%にしたとすると、四捨五入する前の34.375%との差は0.075になって、「秋」よりも影響が大きくなってしまうんだ。
 男の子、はかるのセリフ5
男の子、はかるのセリフ5
ちょうど3分の1ずつに分かれてしまった場合はどうするの?全部33.3%だから順番は付けられないよね。
 コバトンのセリフ18
コバトンのセリフ18
そうだね。そうなるとどうしようもないね。それでもどうしてもと言うなら、正しくないことに目をつぶって三つのうちのどれかを33.4%にするしかないね。
やっぱり、無理に100%に調整しないで注意書きを入れることをおすすめするよ。
うちわけの合計が100%にならないときのグラフの書きかた
 女の子、あやののセリフ5
女の子、あやののセリフ5
でも、帯グラフを書くときはどうするの?合計を100%にしなければ正しいグラフが書けないでしょ。99.9%や100.2%のままだと、はばがそろわないもの。
 コバトンのセリフ19
コバトンのセリフ19
じっさいに帯グラフを書くときは、今説明した合計を100%にするやりかたと同じで、影響(えいきょう)の少ない所で調整するんだ。
例えば合計が100.3%だったら、まず「その他」を0.1小さくする、次に「割合(わりあい)の一番大きい所」を0.1小さくする、その次に「二番目に大きい所」を0.1小さくする、というようにして書けばいいんだ。
全体からみれば、0.1のちがいはほんのわずかだからね。この書きかたで十分正確(せいかく)なグラフが作れるから、そんなに気にしなくても平気だよ。
なぜなら、ふつうの大きさの帯グラフの場合、0.1%のちがいを正確に書くことはかなりむずかしいからなんだ。
たとえば20センチメートルのはばの帯グラフの場合だと、0.1%はたった0.2ミリメートルにしかならないよ。人間だから、かんぺきに同じ太さの線を引くことはできないし、少しもずれることなく定規(じょうぎ)をあてることもできないからね。

